Summary Statistics: Part II

3. Higher Moments

In general, all statistical moments are defined as:

\[ \overline{x^{\prime r}} = \frac{1}{N}\sum_{i=1}^{N}(x_i - \overline{x})^r \]

where \(r\) denotes the moment (e.g. \(r\) = 2 is the variance)

The third and fourth moments are known as the skewness and kurtosis and these describe the shape of a distribution. In practice, these sample moments are typically reported in their standardized form as follows:

\[ \alpha_r = \frac{\overline{x^{\prime r}}}{s^r} \]

where \(s\) is the sample standard deviation.

3.1 Skewness

The skewness (\(r\) = 3) indicates the degree of asymmetry of the distribution about the mean. \(\alpha_3\) > 0 indicates that the distribution has a long tail on the positive side of the mean and \(\alpha_3\) < 0 indicates a long tail on the negative side of the mean. Note a normal distribution has \(\alpha_3\) = 0 (we will discuss the normal distribution in the next section).

3.2 Kurtosis

The kurtosis (\(r\) = 4) describes the shape of a distribution’s tails relative to the rest of the distribution. A normal distribution has \(\alpha_4\) = 3. \(\alpha_4\) > 3 indicates a more peaked distribution compared to normal (leptokurtic) and \(\alpha_4\) < 3 indicates a flatter distribution (platykurtic).

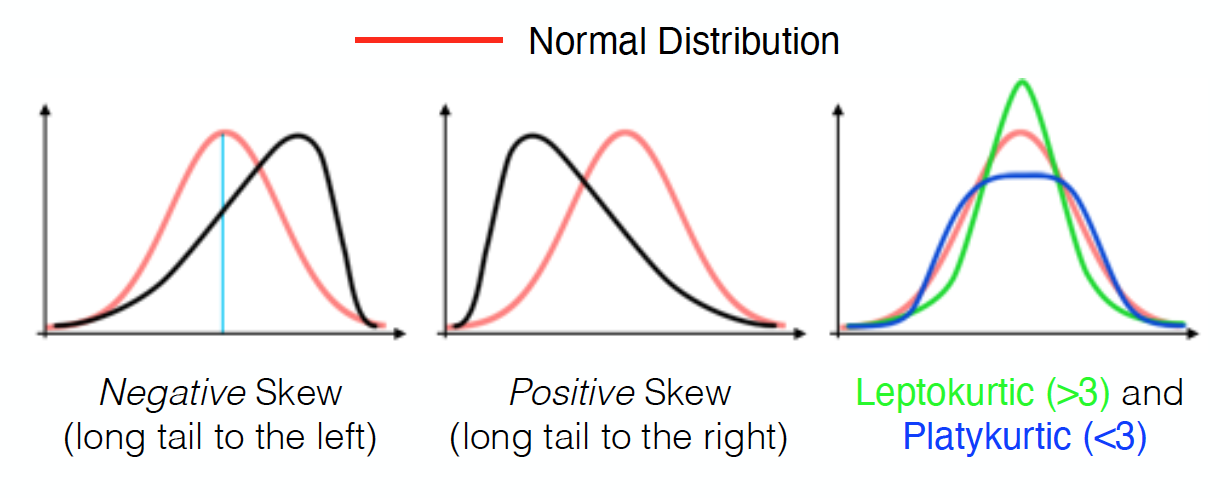
Fig. 5 Negatively and positively skewed and leptokurtic and platykurtic distributions. The normal distribution is shown in red.

Figure 5 contrasts the normal distribution (red) against negatively and positively skewed distributions and leptokurtic and platykurtic distributions.